A glance

精巧的整数类型的结构；
Python 为什么可以表示超长整数？为什么 intel 32 设备上使用 2^30 进制。
Python 整数的理论上限；

Start

整数类型是 Python 最基本的内置对象之一，我们将从这个最简单的对象入手，了解 Python 的面向对对象技术。Python 3 中的整数实现为 PyLongObject，与之关联的几个文件是：

Include/longintrepr.h
Include/longobject.h
Objects/longobject.c

digit 的大小

在 longintrepr.h 定义了 Python 中整数如何表示，其中定义了最关键的类型 digit，这个类型对 Python 表示整数非常重要，最关键的几行代码：

// Include/longintrepr.h
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
#define PyLong_SHIFT    30

当 PYLONG_BITS_IN_DIGIT 为 30 位的时候，digit 和 PyLong_SHIFT 分别为 30 位和 32 位。 PYLONG_BITS_IN_DIGIT 在 Include/pyport.h 中定义：

// Include/pyport.h
#ifndef PYLONG_BITS_IN_DIGIT
#if SIZEOF_VOID_P >= 8
#define PYLONG_BITS_IN_DIGIT 30
#else
#define PYLONG_BITS_IN_DIGIT 15
#endif
#endif

显然 PYLONG_BITS_IN_DIGIT 的大小是根据 SIZEOF_VOID_P 决定的，只要 SIZEOF_VOID_P 不小于 8，PYLONG_BITS_IN_DIGIT 就取 30，否则为 15。 SIZEOF_VOID_P 是什么意思呢？它表示的是操作系统的指针大小，也就是寻址范围，单位是字（8 bit），在 PC/pyconfig.h 可以看到 SIZEOF_VOID_P 的定义，以 Windows 系统为例：

对于 Win32 系统，SIZEOF_VOID_P 为 4，即 4 * 8 = 32 bit；
对于 Win64 系统，SIZEOF_VOID_P 为 8，即 8 * 8 = 64 bit。

因此 digit 在 CPU 寄存器宽度不小于 64 bits 的情况下，为 30 bit，否则只能降低为 15 bits。特别注意 PyLong_SHIFT 在表示任意长度整数时有妙用。

digit 字面意思是数字，而且特指 0～9 中的 1 位数字，可以试想这样一种表示任意整数的方式，将任意整数按照各位 “数字” 保存在一个数组中，比如整数 number = 123456890，16 进制表示为: 0X499602d2，对于 8 位 CPU 是无法直接表示这么大的数字的，这样尝试表示：

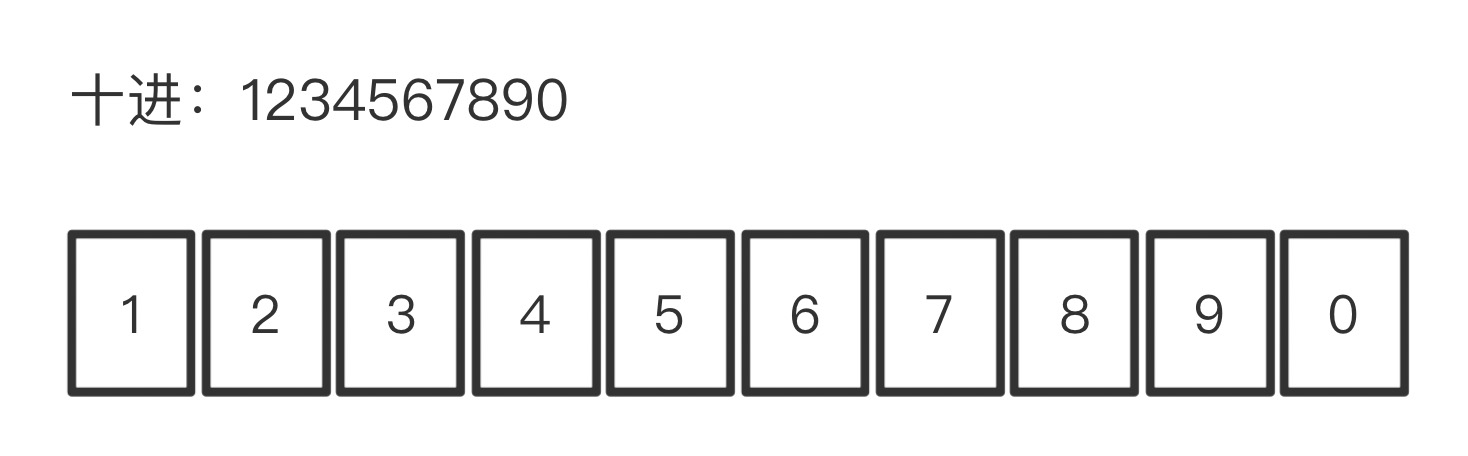
我们将 number 分解为 10 个数字（digit），按位排列保存在一个数组中，这样就可以保存任意位数的整数了。

当然，我们也注意到数组中的每一个元素可以表示的最大正整数为 255，上面的方案只用每一元素表示 0～9，存在巨大的浪费。Python 的方案与此类似，但扩展了对 digit 的定义，在 10 进制中，每一位 digit 的取值范围是 0～9，那么如果是 255（即 2^8）进制，那么每一位 digit 的范围是 0～255，32 位及以上系统中，Python 就使用了 2^30 进制，那么 digit 的范围就是 0～(2^30 - 1)。具体的后面会更进一步了解到。

为什么 digit 是 30 位而不是 32 位

回顾前面提到 digit 表示超长整数的方案，理论上如果希望最大程度利用内存资源，当 Python 运行在 32 位计算机上，那么每一个 digit 应该用 2^32 进制表示数据，这种考虑是正确的，但忽略了 Python 整数对象的目的，Python 中的整数对象不仅仅用于保存数据，更重要的是进行丰富的数学运算，其中最重要的是乘法运算。

二进制中乘法的实现可以利用“左移” 轻松的实现，比如计算 3 * 4，只需要将 3 左移 2 位实现，很少几条 CPU 指令就可以完成。

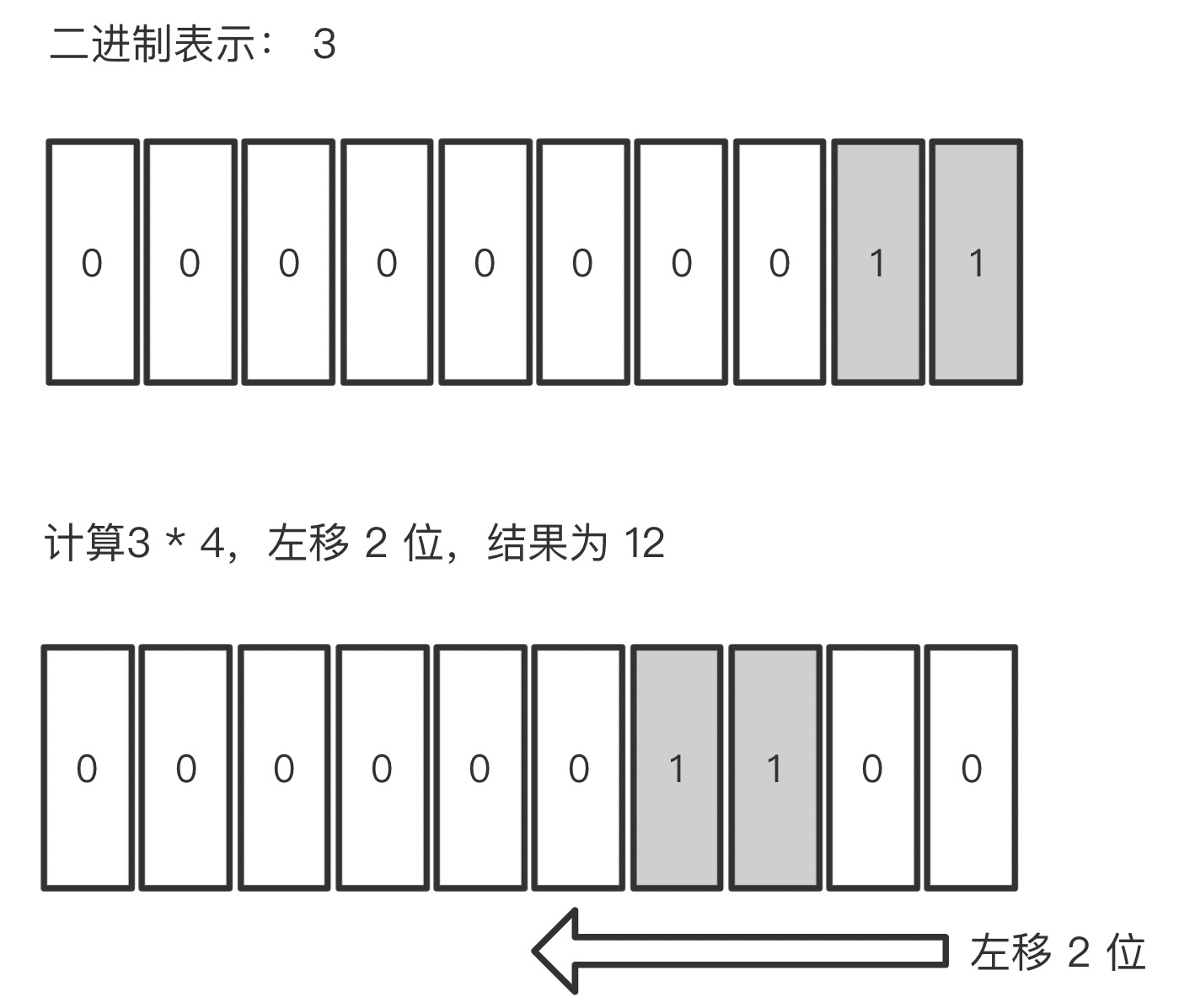
因此，为了方便计算乘法，我们需要预留一半的空间，再加上多保留 1 位用于计算 “溢出”，在 32 位的情况下，就只能用 INT( (32 - 1)/2 ) = 15 位保存数据，64 位系统则使用 32 位系统数据宽度的 2 倍作为数据大小，即 15 * 2 = 30 bits。这样当两个 Python 整数进行运算的时候可以直接按 digit 计算，并且兼顾了 “溢出位”，结果直接保存在一个寄存器中，以获得最佳性能。

整数对象的结构

整数对象是 PyVarObject 的子集，也就是说一个 longobject 拥有 PyVarObject_HEADER，必然也是 PyObject_HEADER.

struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

longobject 看起来像这样：

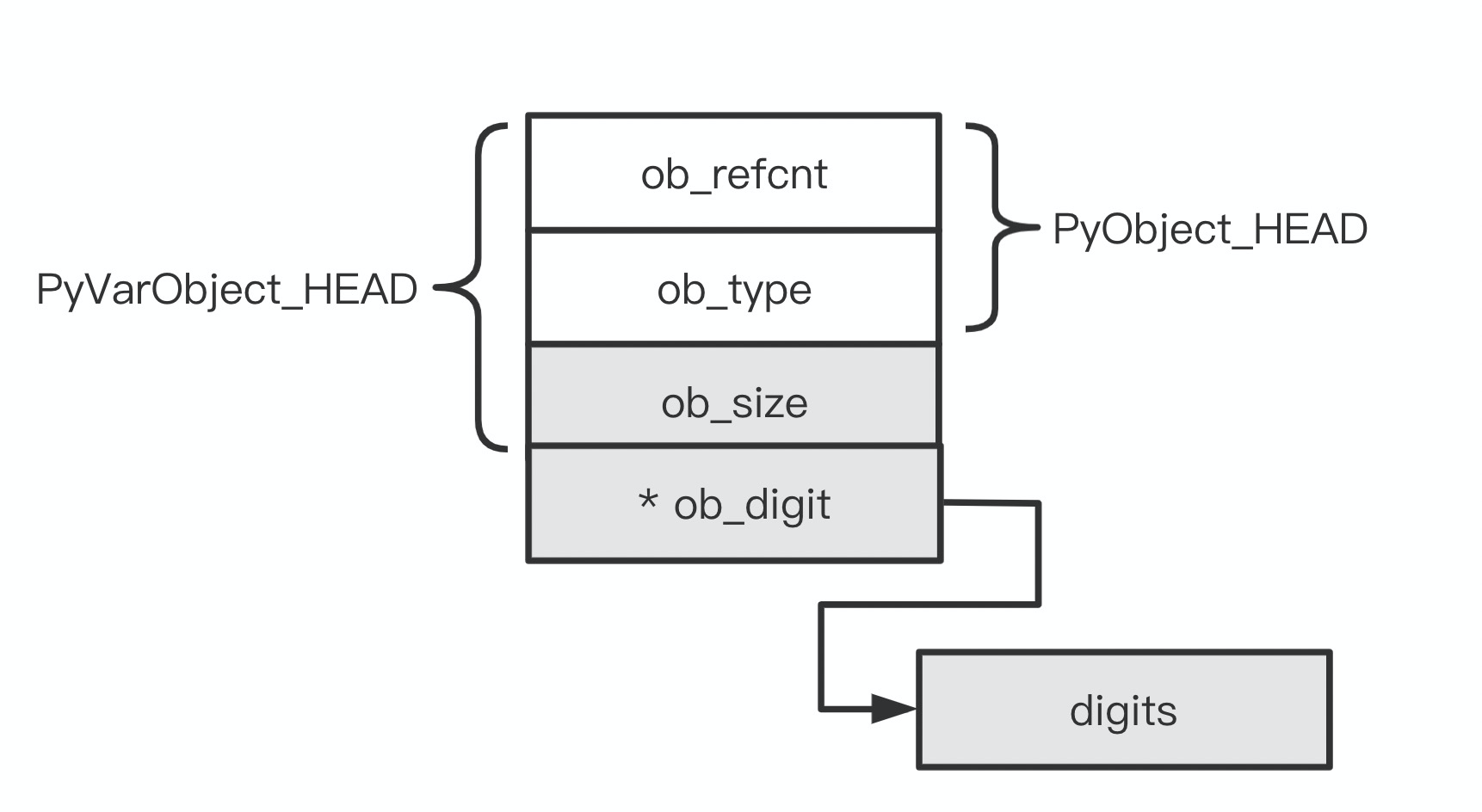
我在图中将所有宏都全部展开了，标注出了头部中不同部分的来源。ob_refcnt 是引用计数；ob_type 是一个指向全局类型对象的指针，对于 longobject 它指向；ob_size 是 longobject 的 digit 数组大小。特别需要注意 ob_size 在 longobject 中存在一些隐式用法，稍后会提到；ob_digit 则是按 2^30 进制分解的 digit 数组。

后面将不再解释 32 位系统与 64 位系统的差异，没有特殊说明，即默认为目前最流行的 64 位系统。

在定义中 ob_digit 的长度明明是 1 啊，为什么还需要 ob_size 呢？实际上 C 语言没有数组越界检查，struct 定义中的数组长度实际并没有直接作用，等效于 digit \ob_digit;* 但这种写法可以清晰的表明这里是一个数组。一个题外话，C 语言中实际上没有真正实现 “数组”，在 C 编译器层面，数组的访问只是简单的 “语法糖”，数组与指针的界限非常模糊，比如下面两段代码可以获得相同的结果：

// 正常
#include <stdio.h>

int main(void) {
    int a[3] = {1,2,3};

    printf("%d\n", 0[a]);
    return 0;
}

// 奇怪的写法

#include <stdio.h>

int main(void) {
    int a[3] = {1,2,3};

    printf("%d\n", 0[a]);
    return 0;
}

实际上 C 语言只是将数组访问简单的转换为 \(array_name + index)*，当然这并不是宏，而是编译器直接实现的。

ob_size 的隐含信息

longobject 的 ob_size 信息同时包含了以下 3 层信息：

是否为 0；
正负极性；
digit 数组长度；

可以用下面的图表示 ob_size 传达的信息：

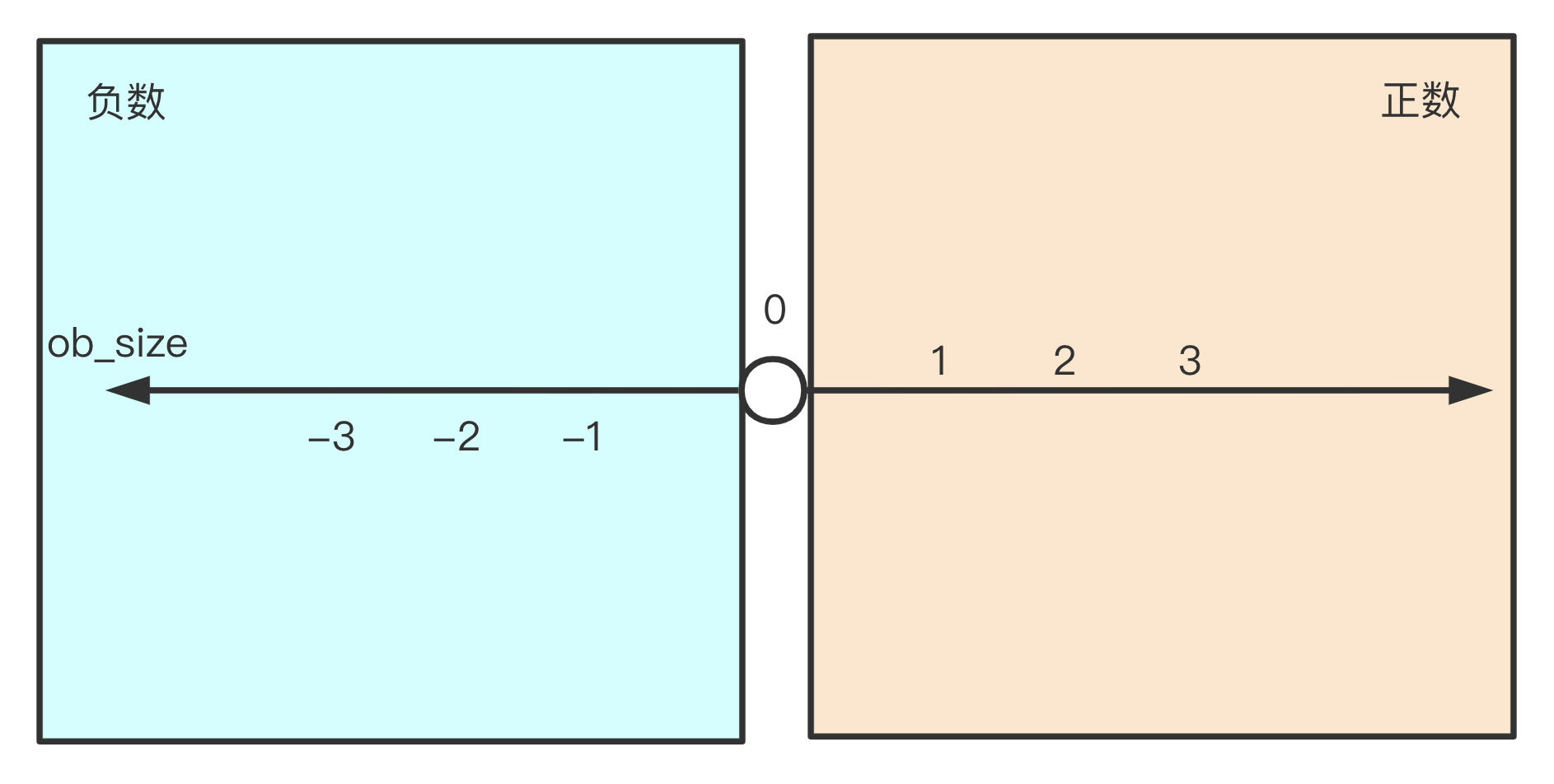
ob_digit 表示的其实是无符号整数，数值的极性由 ob_size 的极性表示，比较特殊的是 ob_size 为 0 即表示数值为 0。ob_size 的绝对值才表示 ob_digit 数组的长度。这样就将数值的极性标志位放在 ob_size 上，简化了 ob_digit 的实现，实际上前面对 ob_digit 的分析都假定它是无符号整数。

同时这里可以大致估算 Python 整数的上限与 ob_size 的上限有关，在 64 位系统中，ob_size 是一个 int64 类型，其绝对值最大的是 -2^63 = -9223372036854775808, 这是 ob_digit 数组长度的理论上限，那么 Python 可以认为是一个采用了 2^30 进制的整数计数系统，那么它能表示的最大整数是 (2^30)^(2^63)，这是一个非常大的数字，可以认为 Python 可以表示任意实用整数了。

整数是最常用的对象，所以 Python 对整数做了一些优化，以提高性能，下一节我们将从整数对象的创建开始探索。

Think In Python

4. Long Object 初探