Python 的长整数乘法使用了 Karatsuba 算法，昨天写的比较粗，今天仔细研究了以下它的实现，真是是妙啊。

多项式乘法

在一切开始之前，需要回顾多项式乘法公式：

(a + b)(c + d) = ac + ad + bc + bd

这是基本的初等数学知识，Karatsuba 算法的实现本质上就是对这个公式的变形。

长整数切分

为了计算长整数的乘法，一种典型的思路是使用分治思想，将长整数切分为较短的部分计算。这里需要注意的是，计算机在计算一个数的 2^n 倍非常快，乘法可以方便的转换为左移 n 位。

对于一个无符号整数 A，可以将其切分高低两部分，假设将其切分为高低 8 位:

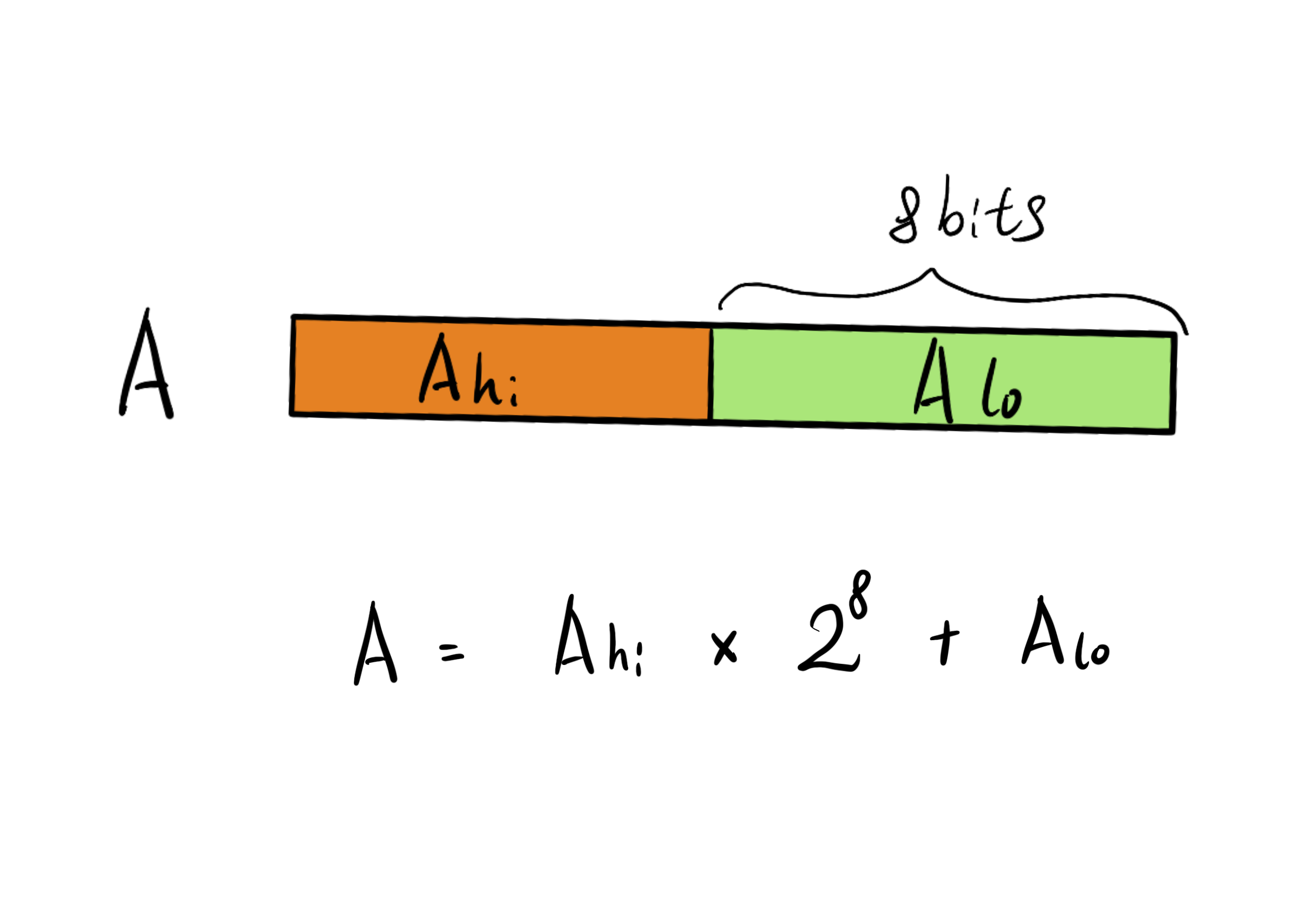
那么 A 就可以表示为 $A_{hi} * 2^n + A_{lo}$，这里 n = 8。实际上 n 可以是任意数值，对于长整数，为了便于计算，通常将 n 设置为较长整数宽度的一半。

由于我们可以将两个长整数按照低位均为 n 位切分：

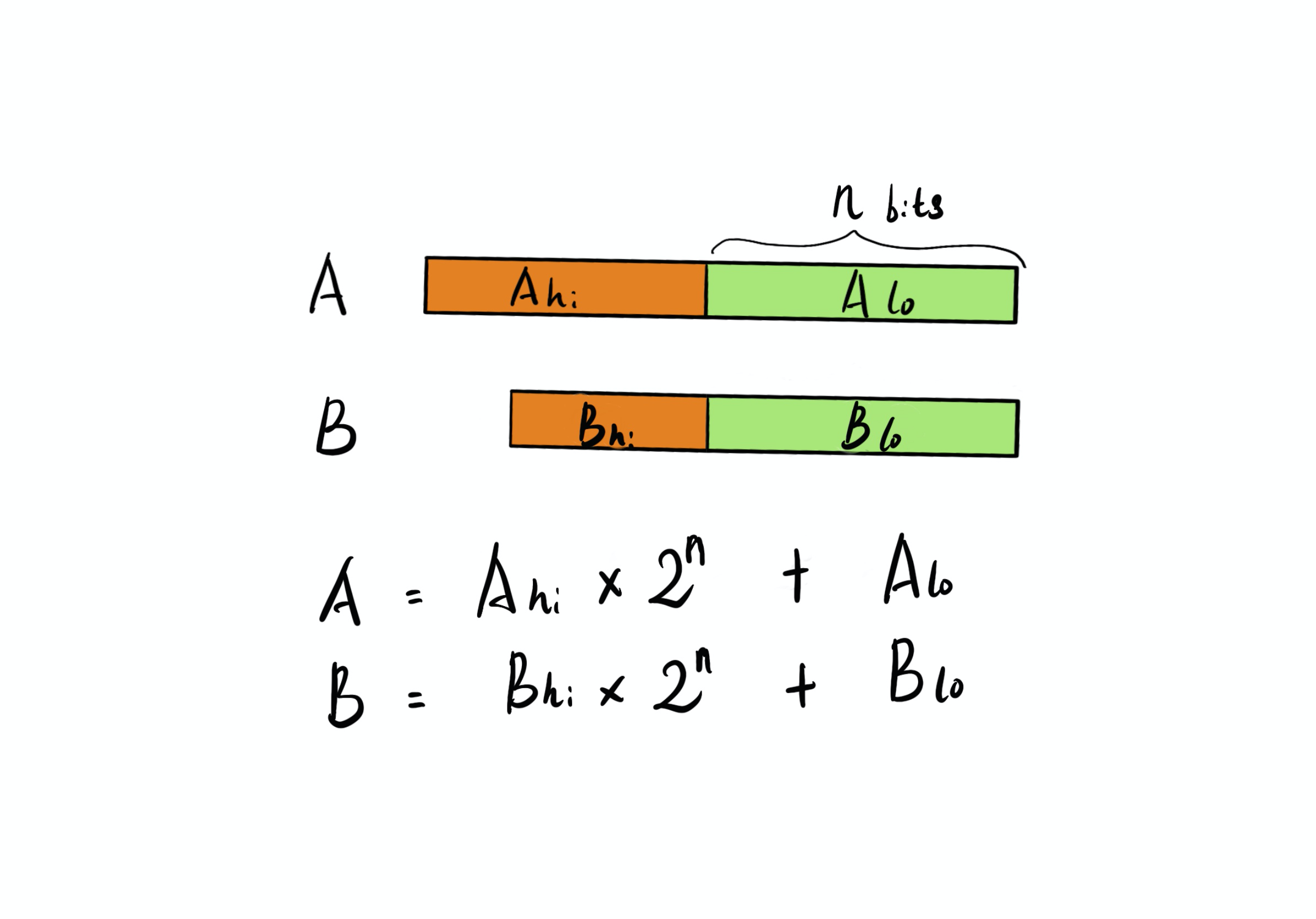
此时 A * B 就是一个多项式乘法：

$$ A B = (A_{hi} X + A_{lo})(B_{hi} X + B_{lo}) $$ $$ = A_{hi} B_{hi} X X + (A_{hi}B_{lo} + A_{lo}B_{hi}) X + A_{lo}B_{lo} $$

$$ = A_{hi} B_{hi} X X + (K - A_{hi}B_{hi} - A_{lo}B_{lo}) X + A_{lo}*B_{lo} $$

其中 $K = (A_{hi} + A_{lo}) * (B_{hi} + B_{lo})$， $X = 2^n$。

这里需要注意一下， $X*X = 2^{n + n}$，回顾前面提到的乘法实现，2^(n + n) 相当于将内存中的值整体左移 2n 位。

首先 Python 申请一个长度为 sizeA + sizeB 的内存 Result，用于保存最终的结果，这一个连续区域被划分为三部分：

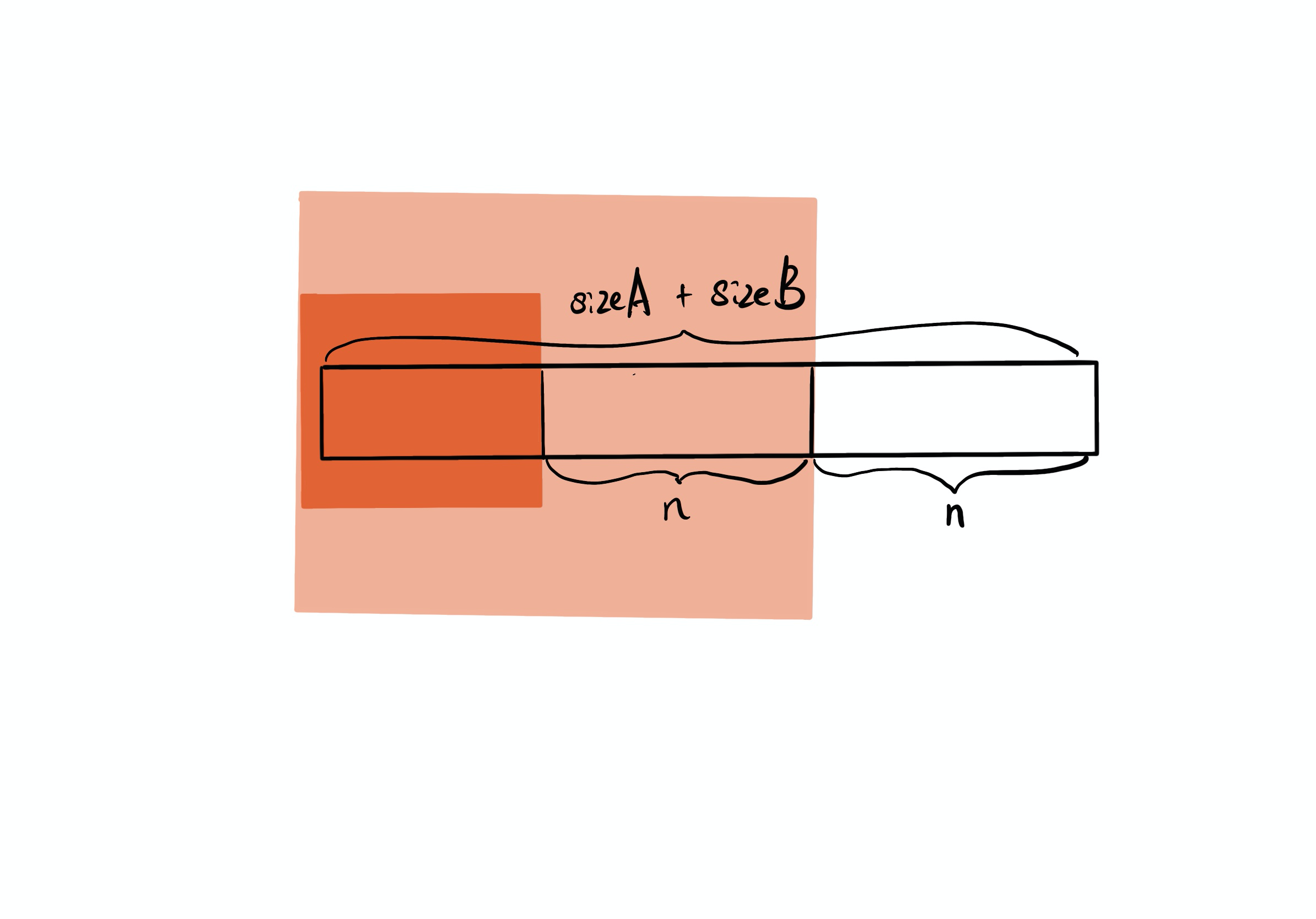
由低到高分别是宽度为 n、n 及剩余的区间，如果对较浅色区域加 X，实际上相当于 Result + X 2^n，在较深区域加 Y，相当于 Result + Y 2^(2n)，这两项刚好是上一部分讲到的多项式乘法的二次项和一次项。

完成结果对象的创建后，首先将 A、B 分割为低位宽度为 n 的两部分，先计算 $A_{hi} B_{hi}$ 并将结果保存到深色区域，对照上一节中的公式，此时 $Result = A_{hi} B_{hi} X X$。

再计算 $A_{lo}B_{lo}$，结果放在最低 n 位，此时 $Result = A_{hi} B_{hi} X X + A_{lo}*B_{lo}$，二次项和常数项都有了，下面是计算中间的一次项。

之后分别将 $- A_{hi}B_{hi}$ 和 $- A_{lo}B_{lo}$ 的结果加到左移 n 的位置，内存看起来是这样：

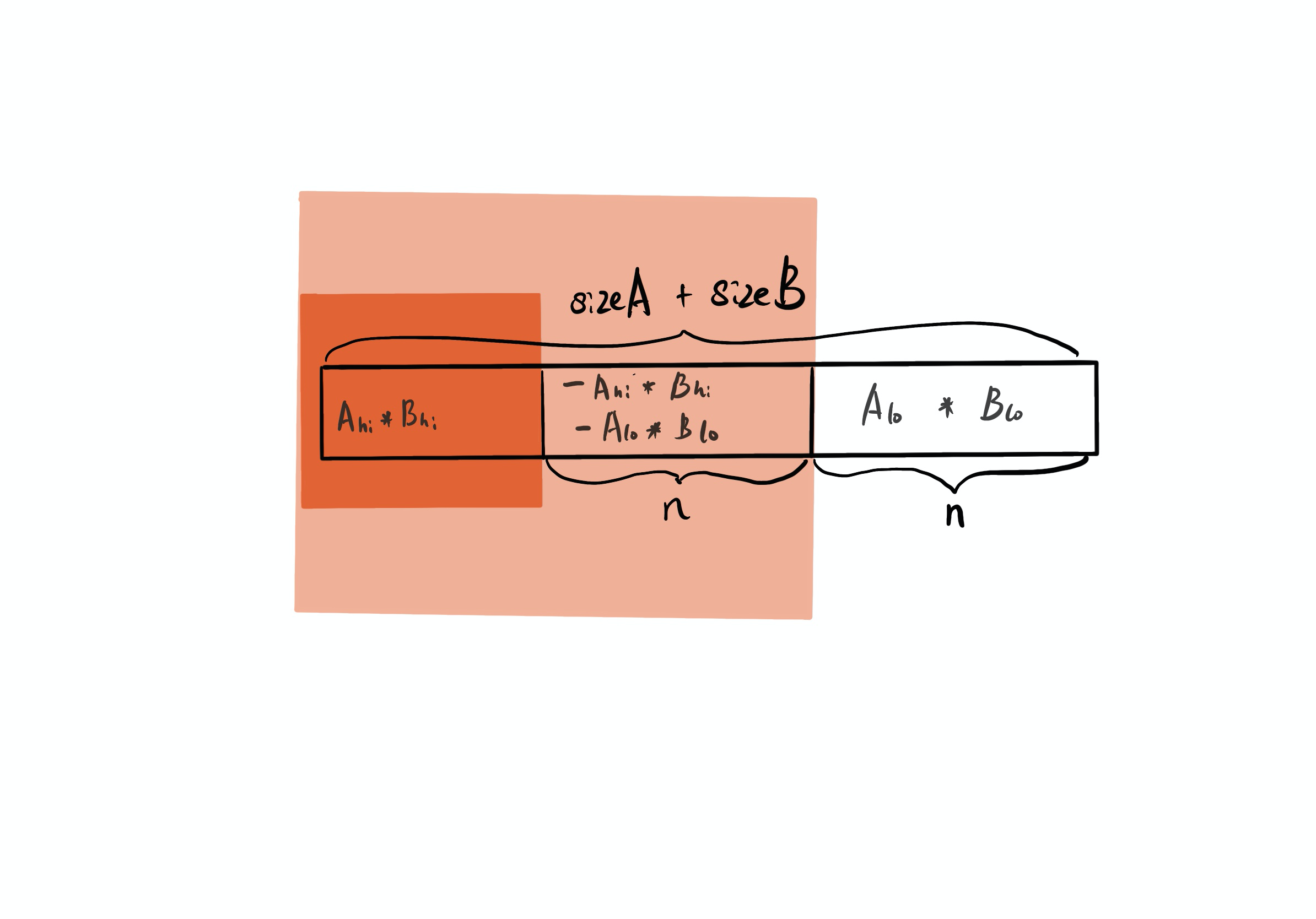
此时

$$ Result = A_{hi} B_{hi} X X + (- A_{hi}B_{hi} - A_{lo}B_{lo}) X + A_{lo}*B_{lo} $$

可以看到这种内存布局的巧妙之处，三段内存独立求和，假如存在进位，刚好自动计入更高分片。对比完整公式，还欠缺一次项的 K。

最后在左移 n 位的位置加 K，就得到了最终的乘法结果。