创建 SetObject
向 Set 增加元素
从 Set 中 pop 元素
Set 的 lookup

让我们再次请出 PySetObject 图示：

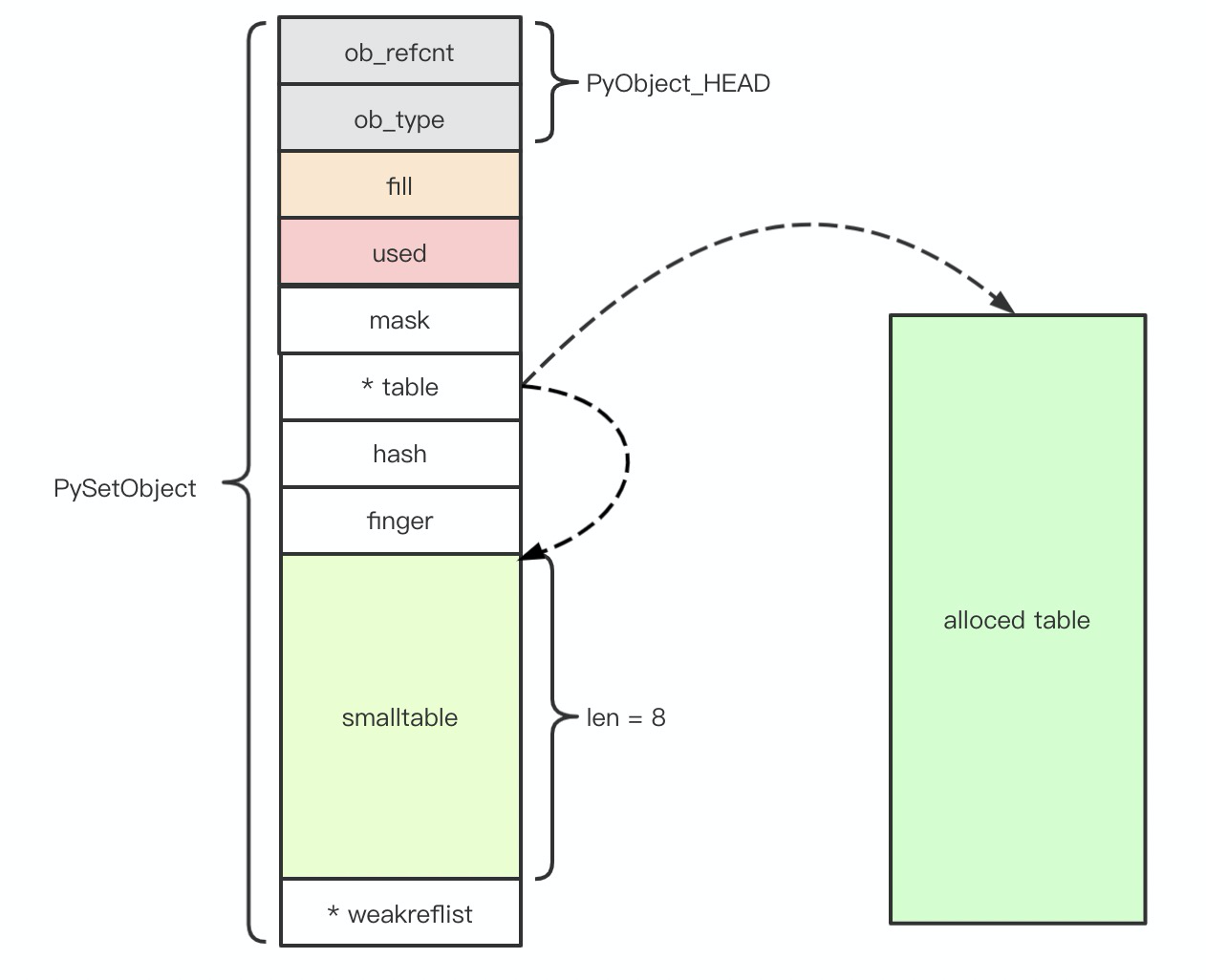
其中最关键的是：

fill：有效元素 + dummy 元素数量，dummy 元素与 Dict 中类似，是删除元素的遗迹。
used: 实际有效元素数量。

Set 采用与 Dict 相似的哈希算法，对数据的删除策略也很相似，已删除数据在哈希表中的位置，会被设置为 dummy。换句话说，如果 fill == used，就说明整个 Set 中没有 dummy 元素，但是这不意味这 Set 从来没有删除过数据，因为 dummy 元素可能被在某些时候被新的有效值覆盖。

创建 SetObject

一切还是从源头开始，按照 Python 的编码规范，创建 Set 的顶级函数为 PySet_New，其最终调用的是：

// Objects/setobject.c:1024

static PyObject *
make_new_set(PyTypeObject *type, PyObject *iterable)
{
    PySetObject *so;
    // 调用 PySet_Type 的构造函数
    so = (PySetObject *)type->tp_alloc(type, 0);
    if (so == NULL)
        return NULL;
    // 简单的初始化对象
    so->fill = 0;
    so->used = 0;
    so->mask = PySet_MINSIZE - 1;
    so->table = so->smalltable;
    so->hash = -1;
    so->finger = 0;
    so->weakreflist = NULL;

    // ··· ···
    // 利用传入的 iter 初始化 Set 的内容。

    return (PyObject *)so;
}

如果预料的一样， PySet_MINSIZE 是 8，也就是 Set 初始化的 smalltable 尺寸。PySet_MINSIZE 同时也被应用于计算 Set 的 mask 成员，这个 mask 的作用是用来对元素的 hash 值对哈希表长度求 mod，方法也很简单：

    i = hash & Set->mask

在源码中会在很多地方见到类似的代码。另外，mask 成员也被用来控制对哈希表的遍历，比如：

    for(int i = 0; i <= Set->mask; i++){
         // do something.
    }

Set 在创建之初，就将 table 指向自身尾巴上的 smalltable：

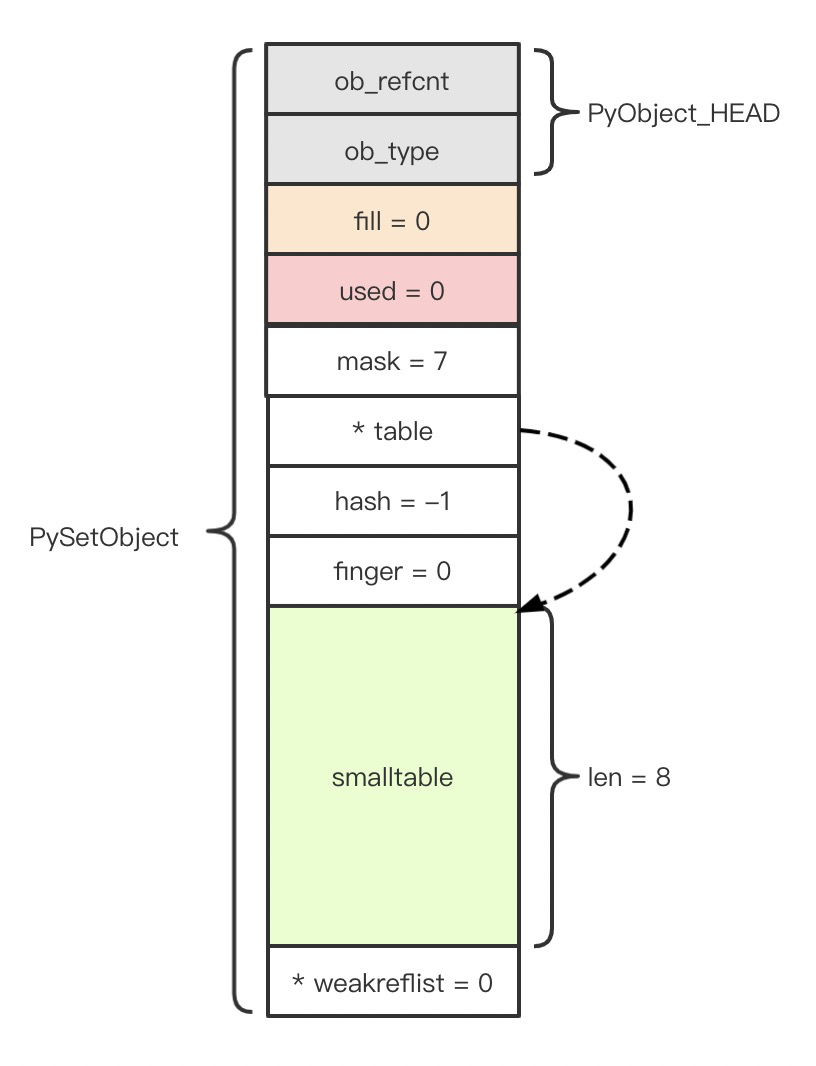
这样做的好处是，对于任意 Set，它的 table 都有有效值，可以免去大量的检测代码。

Set 的 table 集合了哈希和 Key 存储两种功能，随着元素的增加，哈希表的碰撞性能会快速下降，因此哈希表并不会等到哈希表用尽才进行伸缩，与 Dict 中的结论一样，实践证明当哈希表的装载率超过 2/3 性能就会迅速下降。在新增 entry 的函数中有这样的代码：

// Objects/setobject.c:246

static int
set_add_entry(PySetObject *so, PyObject *key, Py_hash_t hash){

    // ··· ···

    // 如果当前已占用元素超过哈希表的 3/5，就伸缩 table 的尺寸
    if ((size_t)so->fill*5 < mask*3)
        return 0;
    return set_table_resize(so, so->used>50000 ? so->used*2 : so->used*4);

}

在新增元素时，会检查当前 table 的装载率，如果已经超过 3/5，就进行伸缩，当有效元素数量不超过 50000，就扩充到 4 倍有效元素，否则就只阔从到 2 倍，节约一点内存。

对 table 调整大小的尝试，会发生在每一次新增元素的时候。只要实际需要的 table 尺寸大于 8，Set 就会申请独立的内存块，并将 smalltable 里的 entry 插入到新的哈希表中，后面哈希表就跟 Set 的本体分割开了。

向 Set 增加元素

无论哈希表位于 smalltable 还是一块独立的内存都没关系，我们只需要关注 table 指针就可以了，如没有特别需要，后面我将不再具体说明哈希表到底在哪里，这不会引起其他的副作用。

向 Set 中增加元素的过程是：

在哈希表中找到第一个空闲或者 dummy 位置，
设置该位置 entry.key 为插入的 Key 即可。

这个搜索过程类似 Dict 的 lookup 函数，但稍有不同，可以分为：

计算哈希表中的起始探测位置 i = (size_t)hash & mask；
线性探测阶段，检查 Set->table[i] 及之后 9 个元素，共计 10 个相邻元素；
哈希探测阶段，根据公式计算二次探测点 i，重复步骤 2；

对于某个长度为 32 的哈希表：

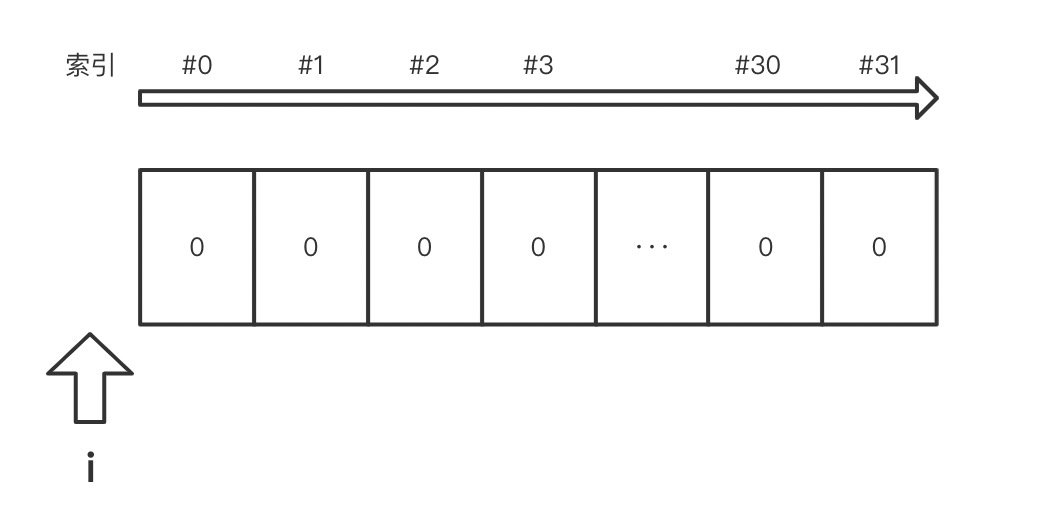
对应的，它的 mask = 32 - 1 = 31.

我用白色区域表示哈希表中的空闲 entry，后面会用绿色表示有效 entry，红色表示 dummy entry。为了方便，我们直接使用数字作为 Key，因为数字的 hash 就是其自身。

假定该 Set 名称为 a。

首先执行 a.add(1) :

i = 1 & 31 = 1;
检查 table[1]，空闲，该位置可以储存 Key;
将 table[1].key 设置为 1.

此时 table 看起来这样：

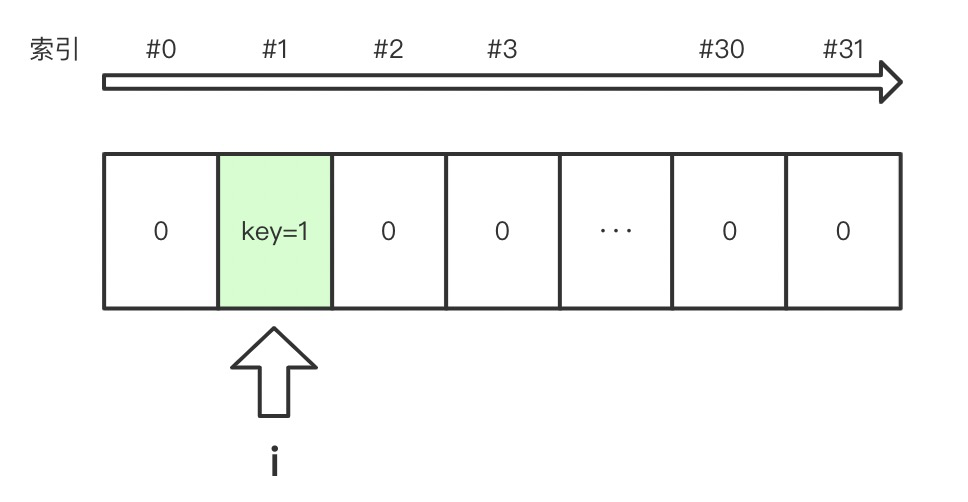
下面我们继续插入一个冲突元素：a.add(33)：

i = 33 & 31 = 1；
检查 table[1]，占用。
进入线性探测，检查下一位置 table[i+1]，空闲；
将 table[2].key 设置为 33.

此时 table 看起来；

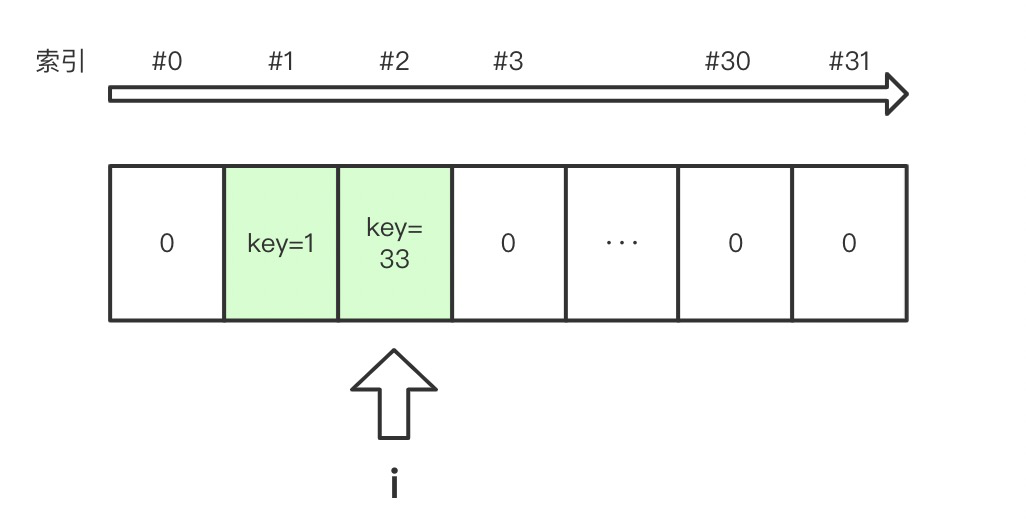
如果连续不断的向 a 插入碰撞在同一位置的 Key，比如 32*n + 1 这样的 Key，那么它们会在 table[1] ~ table[10] 连续排列。当然，如果在期间插入过其他的 Key，则有可能会被插入到它们之间的某个位置。

线性探测阶段最多只检查从哈希位置开始的 10 个元素，如果一直没有找到可用 entry，那么就开始再次哈希，其计算公式与 Dict 的二次探测公式类似：

perturb >>= PERTURB_SHIFT;
i = (i * 5 + 1 + perturb) & mask;

它的作用是将结果均匀的散列在哈希表中，这里不再详细展开。从 Key 的插入过程可以大概了解 Set 的遍历顺序是如何确定的。

从 Set 中 pop 元素

由于 Set 的实现使用了哈希表，为了解决哈希碰撞的问题，使用了一些策略形成探测链，所以在对 Set 删除的时候，实际上只能将其标记删除，而不能真的将 entry.key 设置为 NULL。其搜索步骤与插入元素类似，但查找目标是 entry == Key 的位置，先后经过：

计算哈希 i;
线性探测阶段；
计算探测链上的下一个位置，进行二次哈希探测；

只要这个 Key 出现在 Set 中，就会很快找到这个 entry，然后 entry.key = dummy, dummy 是一个全局对象，完成对这个 entry 的一些重置工作，删除动作就结束了。

删除某个 entry 后，table 看起来如此：

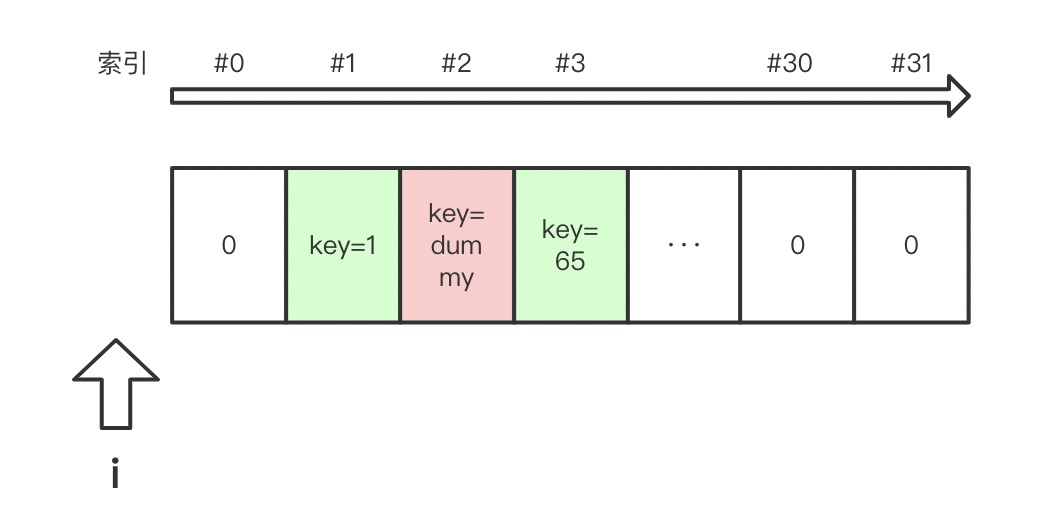
Set 的 lookup

对 Set 的基本增删操作中，包含了实质上的 lookup 操作，这些都会在其他高级操作中被高度复用。

Think In Python

46. Set 是如何工作的(2)

创建 SetObject

向 Set 增加元素

从 Set 中 pop 元素

Set 的 lookup